微分
微分学的核心思想:用熟悉且简单的函数对复杂函数进行局部逼近
基本的概念
常用来逼近的函数
- 线性函数:函数的一阶导数()
- 多项式函数:泰勒级数
极限定义(描述)
自然语言:当x趋于a时,f(x)的极限是L。
数学符号:
标准语言(术语,严格证明时用):
对于任意的$\varepsilon > 0$,存在一个$\delta > 0$,使得对于任何$x_{*} \epsilon (a - \delta, a + \delta)$,都有$\left | f(x) - L \right | < \varepsilon$
无穷小
定义:一般把趋于零的极限称为无穷小。
无穷小阶数:
趋于零的速度越快的无穷小,其阶数越高。比$x^n, x \rightarrow 0$(n阶无穷小),趋于零速度还快的无穷小记为$o(x^n)$
两边夹定理
如果$f(x) < g(x) < h(x)$,而且这三个函数都在a点处有极限,那么
- 由两边夹定理推导出的结论
- 三角函数:$\lim_{x \rightarrow 0} \frac{sin(x)}{x} = 1$
- 指数函数:$\lim_{x \rightarrow 0} \frac{e^x - 1}{x} = 1$
- 自然对数底数:$e = \lim_{x \rightarrow 0} (1 + \frac{1}{n})^n$
下面是一些证明过程
三角函数:$\lim_{x \rightarrow 0} \frac{sin(x)}{x} = 1$
借助直角坐标系来完成这个证明,请看图: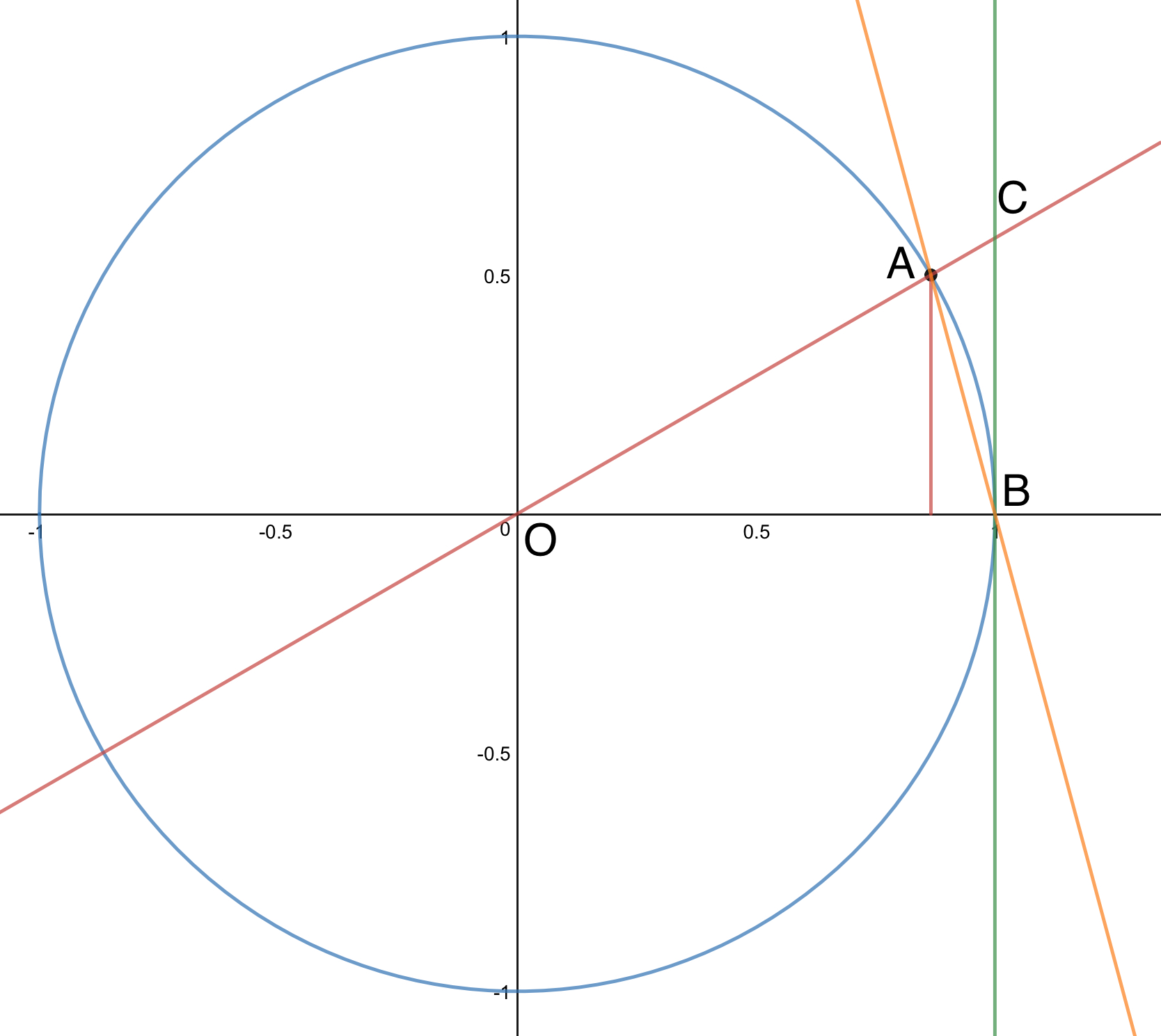
如图,我们可以得出结论,面积相比 三角形AOB < 扇形AOB < 三角形BOC
假设为x,那么弧AB为x,同时容易得出
三角形AOB的面积为
扇形AOB面积为
三角形BOC面积为
根据观察得出的结论,可以得到
因为x是大于0的数,并且我们想研究的数为,所以同时除以x,有,可以转化为
将两个小于号拆开可以得到: 和 ,后者可以化简为
结合两者,可以推出:
最后,因为 且 ,根据两边夹定理,可以得出
先看,根据定义可知:
令:,则有:
令: ,则可以写成
而可以根据二项式展开写成:
二项式展开公式:
组合公式:
排列公式:
所以把刚刚二项式展开的公式中的都替换成就有:
化简得
上式对的化简:
根据两边夹定理,得证$\lim_{x \rightarrow 0} \frac{e^x - 1}{x} = 1$
求导
导数是什么: 导数也是极限
一元函数
一阶导数定义:
- 几何意义:用直线逼近曲线
- 代数意义:用线性函数逼近复杂函数
常见函数的导数:
(C为常数)
n阶导数
二阶导数: 导数的导数就是二阶导数
n阶导数: 就是导数的n次导数…
Taylor级数(对函数进行高阶逼近):
如果一个函数是n阶可微函数, 那么:
函数的n阶Taylor级数就是与拥有相同前n阶导数的n阶多项式
为什么要做Taylor展开:
因为微分的思想是逼近, 而我们自然会想到, 用多少阶导数去逼近呢? 如果使用一阶导数, 也就是线性逼近的话, 误差会不会大, 如果是使用高阶导数, 那么计算会变得复杂。
而Taylor级数告诉了我们一个很重要的道理:
当我们做n阶Taylor展开时, 最终的误差会缩小到这个量级.
也就是说, 当我们使用线性逼近的时候,误差会是o()这个量级, 而当我们做二阶Taylor展开时, 误差会缩小到这个量级.
多元函数
对于一个二元函数, 偏导数定义为:
式子看上去很复杂, 实际上就是对一个参数求偏导时, 把另外不含这个参数的变量看成常数
之所以叫偏导数, 是因为它只是代表了这个函数的一部分导数.
比如说: 是函数 沿着x轴上的导数.
而函数 沿着方向方向的导数为
所以,实际上偏导数就是沿着坐标轴方向的方向导数!
梯度
而我们把两个偏导数求出来后, 组成的向量 , 则称为这个函数的梯度
梯度的代数意义: 对函数进行线性逼近
梯度的几何意义:
梯度方向就是函数增长最快的方向!!!
梯度方向就是函数增长最快的方向!!!
梯度方向就是函数增长最快的方向!!!
(重要的事情说3遍, 为啥呢, 下次就知道了)